Eunjung Kim
Erdos-Posa Property of Chordless Cycles and its Applications
VCLA hosted a talk by Eunjung Kim
| DATE: | Tuesday, December 19, 2017 |
| TIME: | 16:00 s.t. |
| VENUE: | Library, Favoritenstraße 9-11, Stairs 2, Floor 4 (HB 04 08) |
ABSTRACT
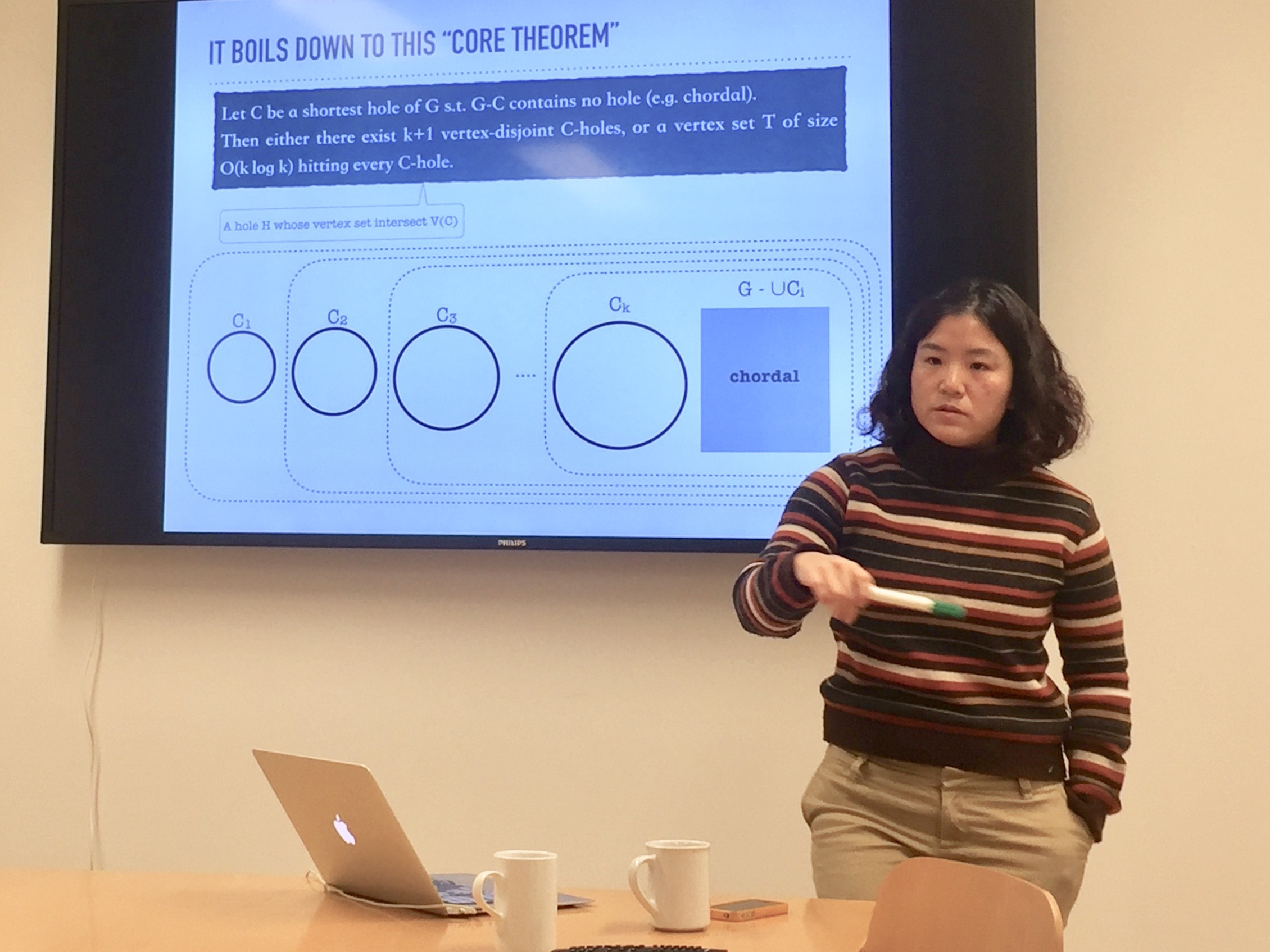
A chordless cycle is a cycle of length at least 4 that has no chord. We prove that the class of all chordless cycles has the Erdos-Posa property, which resolves the major open question concerning the Erdos-Posa property. We complement our main result by showing that the class of all chordless cycles of length at least l for any fixed l ≥ 5 does not have the Erdos-Posa property.
Our proof for chordless cycles is constructive: in polynomial time, one can either find k + 1 vertex-disjoint chordless cycles, or ck2 log k vertices hitting every chordless cycle for some constant c. It immediately implies an approximation algorithm of factor O(opt log opt) for Chordal Vertex Deletion, which improves the best known approximation by Agrawal et. al. The improved approximation algorithm entails improvement over the known kernelization for Chordal Vertex Deletion.
As a corollary, for a non-negative integral function w defined on the vertex set of a graph G, the minimum value sum_{xin S} w(x) over all vertex sets S where G − S is forest is at most O(k2 log k) where k is the maximum number of cycles (not necessarily vertex-disjoint) in G such that each vertex v is used at most w(v) times.